Question

The normal boiling point of a liquid is 282 °C. At what temperature (in °C) would the vapor pressure be 0.350 atm? (∆Hvap = 28.5 kJ/mol)

Answer 1

Using the Clausius-Clapeyron equation, which relates the vapor pressure and temperature of a liquid, we can calculate the temperature corresponding to a vapor pressure of 0.350 atm given the normal boiling point and the heat of vaporization.

Step-by-step explanation:

The student's question pertains to the relationship between the vapor pressure of a liquid and its temperature, specifically when the vapor pressure is different from the pressure at the liquid's normal boiling point. To calculate the temperature at a vapor pressure different from 1 atm, we use the Clausius-Clapeyron equation, which relates the change in the vapor pressure of a liquid to its change in temperature. In this scenario, we know the normal boiling point (282 °C), the enthalpy of vaporization (ΔHvap = 28.5 kJ/mol), and we are given the vapor pressure (0.350 atm) for which we need to find the corresponding temperature.

The Clausius-Clapeyron equation is expressed as:

ln(P2/P1) = -ΔHvap/R × (1/T2 - 1/T1)

where P1 and T1 are the vapor pressure and temperature at the normal boiling point, P2 and T2 are the vapor pressure and temperature we want to find, ΔHvap is the enthalpy of vaporization, and R is the ideal gas constant (8.314 J/(mol·K)). By rearranging the equation and solving for T2, we can determine the temperature at which the vapor pressure of the liquid is 0.350 atm.

Answer 2

The temperature at which the vapor pressure would be 0.350 atm is 201.37°C

Step-by-step explanation:

The relationship between variables in equilibrium between phases of one component system e.g liquid and vapor, solid and vapor , solid and liquid can be obtained from a thermodynamic relationship called Clapeyron equation.

Clausius- Clapeyron Equation can be put in a more convenient form applicable to vaporization and sublimation equilibria in which one of the two phases is gaseous.

The equation for Clausius- Clapeyron Equation can be expressed as:

`\mathtt{In (P_2)/(P_1)= (\Delta \ H _(vap))/(R) \begin {pmatrix} (T_2 -T_1)/(T_2 \ T_1) \end {pmatrix} }`

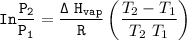
where ;

`P_1` is the vapor pressure at temperature 1

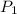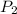`P_ 2` is the vapor pressure at temperature 2

∆Hvap = enthalpy of vaporization

R = universal gas constant

Given that:

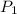`P_1` = 1 atm

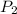`P_ 2` = 0.350 atm

∆Hvap = 28.5 kJ/mol = 28.5 × 10³ J/mol

`T_1` = 282 °C = (282 + 273) K = 555 K

R = 8.314 J/mol/k

Substituting the above values into the Clausius - Clapeyron equation, we have:

`\mathtt{In (P_2)/(P_1)= (\Delta \ H _(vap))/(R) \begin {pmatrix} (T_2 -T_1)/(T_2 \ T_1) \end {pmatrix} }`

`\mathtt{In \begin {pmatrix} (0.350)/(1) \end {pmatrix} } = (28.5 * 10^3 )/( 8.314 ) \begin {pmatrix} (T_2 - 555)/(555T_2) \end {pmatrix} }`

`\mathtt{In \begin {pmatrix} (0.350)/(1) \end {pmatrix} } = (28.5 * 10^3 )/( 8.314 ) \begin {pmatrix} (1)/(555)- (1)/(T_2) \end {pmatrix} }`

`- 1.0498= 3427.953 \begin {pmatrix} (1)/(555)- (1)/(T_2) \end {pmatrix} }`

`(- 1.0498)/(3427.953)= \begin {pmatrix} (1)/(555)- (1)/(T_2) \end {pmatrix} }`

`- 3.06246906 * 10^(-4)= \begin {pmatrix} (1)/(555)- (1)/(T_2) \end {pmatrix} }`

`(1)/(T_2) = \begin {pmatrix} (1)/(555)+ (3.06246906 * 10^(-4) ) \end {pmatrix} }`

`(1)/(T_2) = 0.002108048708`

`T_2 = (1)/(0.002108048708)`

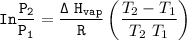
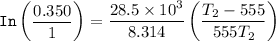
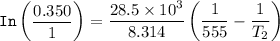
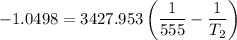
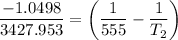
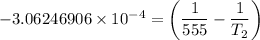
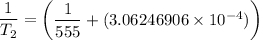
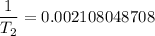
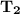`\mathbf{T_2 }` = 474.37 K

To °C ; we have
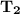`\mathbf{T_2 }` = (474.37 - 273)°C

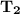`\mathbf{T_2 }` = 201.37 °C

Thus, the temperature at which the vapor pressure would be 0.350 atm is 201.37 °C