Complete Question
The complete question is shown on the first uploaded image
Answer:
The differential equation that fits the physical description is
![(d (v(t)))/(dt) = z [v(t)]^2](https://img.qammunity.org/2021/formulas/mathematics/college/2to20e4amvo6h3ktqobhxzgwem8lagyy6r.png)
Explanation:
From the question we are told that
The acceleration due to air resistance of a particle moving along a straight line at time t is proportional to the second power of its velocity v, this can be mathematically represented as
![a(t) \ \ \alpha \ \ \ [v(t)]^2](https://img.qammunity.org/2021/formulas/mathematics/college/yn6bm4isrcwz86zgo24u6a7n1q1f12ix0g.png)
Where
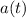 is the acceleration at time t
is the acceleration at time t
and
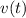 is the velocity at time t
is the velocity at time t
So
=>
![a(t)= z [v(t)]^2](https://img.qammunity.org/2021/formulas/mathematics/college/fz7u6dx7i960vimzjdc8plhaiwj12esja7.png)
Where z is a constant
Generally acceleration is mathematically represented as

So
![(d (v(t)))/(dt) = z [v(t)]^2](https://img.qammunity.org/2021/formulas/mathematics/college/2to20e4amvo6h3ktqobhxzgwem8lagyy6r.png)