Answer:
(A). The direction of the induced current will be clockwise.
(B). The magnitude of the average induced emf 16.87 mV.
(C). The induced current is 6.75 mA.
Step-by-step explanation:
Given that,
Magnetic field = 0.45 T
The loop's diameter changes from 17.0 cm to 6.0 cm .
Time = 0.53 sec
(A). We need to find the direction of the induced current.
Using Lenz law
If the direction of magnetic field shows into the paper then the direction of the induced current will be clockwise.
(B). We need to calculate the magnetic flux
Using formula of flux
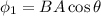
Put the value into the formula
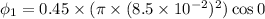

We need to calculate the magnetic flux
Using formula of flux
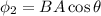
Put the value into the formula
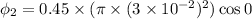
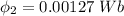
We need to calculate the magnitude of the average induced emf
Using formula of emf
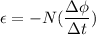
Put the value into t5he formula
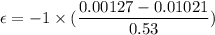
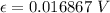
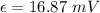
(C). If the coil resistance is 2.5 Ω.
We need to calculate the induced current
Using formula of current

Put the value into the formula
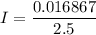

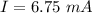
Hence, (A). The direction of the induced current will be clockwise.
(B). The magnitude of the average induced emf 16.87 mV.
(C). The induced current is 6.75 mA.