Answer and Step-by-step explanation: Spherical coordinate describes a location of a point in space: one distance (ρ) and two angles (Ф,θ).To transform cartesian coordinates into spherical coordinates:
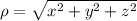
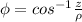
For angle θ:
- If x > 0 and y > 0:
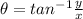 ;
;
- If x < 0:
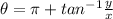 ;
; - If x > 0 and y < 0:
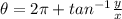 ;
;
Calculating:
a) (4,2,-4)
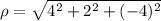 = 6
= 6
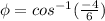
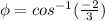
For θ, choose 1st option:
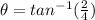
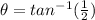
b) (0,8,15)
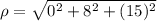 = 17
= 17
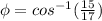
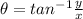
The angle θ gives a tangent that doesn't exist. Analysing table of sine, cosine and tangent: θ =
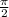
c) (√2,1,1)
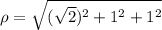 = 2
= 2
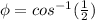
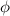 =
=
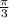
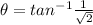
d) (−2√3,−2,3)
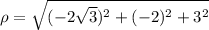 = 5
= 5
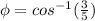
Since x < 0, use 2nd option:
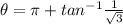
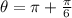
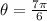
Cilindrical coordinate describes a 3 dimension space: 2 distances (r and z) and 1 angle (θ). To express cartesian coordinates into cilindrical:
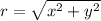
Angle θ is the same as spherical coordinate;
z = z
Calculating:
a) (4,2,-4)
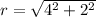 =
=
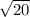
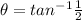
z = -4
b) (0, 8, 15)
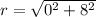 = 8
= 8
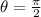
z = 15
c) (√2,1,1)
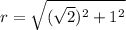 =
=
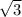
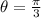
z = 1
d) (−2√3,−2,3)
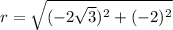 = 4
= 4
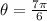
z = 3