Question

15. For a random sample of n = 64, find the probability of a sample mean being

less than 24.3 when p = 24 and o = 1.25.

Answer 1

0.9726

Step-by-step explanation:

The computation of the probability of a sample mean is shown below:

`P(\bar x < 24.3)`

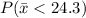
To find the probability first we have to determine the z score which is

`z = (\bar x - \mu_(\bar x))/(\sigma_(\bar x)) \\\\ = (\bar x - \mu )/((\sigma)/(√(n) ) ) \\\\ = (24.3 - 24)/((1.25)/(√(64) ) )`

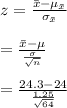
= 1.92

Now probability is

`P(\bar x < 24.3) \\\\= P(z < 1.92)`

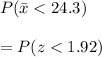
= 0.9726

Hence, the probability of the sample mean is 0.9726

We simply applied the above formulas to determined the probability of a sample mean and the same is to be considered