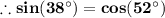Question

Use the diagram to complete the statement. Triangle J K L is shown. Angle K J L is a right angle. Angle J K L is 52 degrees and angle K L J is 38 degrees. Given △JKL, sin(38°) equals cos(38°). cos(52°). tan(38°). tan(52°).

Answer 1

`\bold{sin(38^\circ)=cos(52^\circ)}`

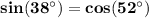
Explanation:

Given that
`\triangle KJL` is a right angled triangle.

`\angle JKL = 52^\circ\\\angle KLJ = 38^\circ`

and

`\angle KJL = 90^\circ`

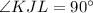
Kindly refer to the attached image of
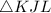`\triangle KJL` in which all the given angles are shown.

To find:

sin(38°) = ?

a) cos(38°)

b) cos(52°)

c) tan(38°)

d) tan(52°)

Solution:

Let us use the trigonometric identities in the given
`\triangle KJL`.

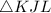We have to find the value of sin(38°).

We know that sine trigonometric identity is given as:

`sin\theta =(Perpendicular)/(Hypotenuse)`

`sin(\angle JLK) = (JK)/(KL)\\OR\\sin(38^\circ) = (JK)/(KL)`....... (1)

Now, let us find out the values of trigonometric functions given in options one by one:

`cos\theta =(Base)/(Hypotenuse)`

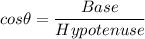
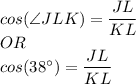`cos(\angle JLK) = (JL)/(KL)\\OR\\cos(38^\circ) = (JL)/(KL)`....... (2)

By (1) and (2):

sin(38°)
`\\eq` cos(38°).

`cos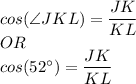(\angle JKL) = (JK)/(KL)\\OR\\cos(52^\circ) = (JK)/(KL)` ...... (3)

Comparing equations (1) and (3):

we get the both are same.

`\therefore \bold{sin(38^\circ)=cos(52^\circ)}`