Question

The volume of ice-cream in the cone is half the volume of the cone. The cone has a 3 cm radius and

6 cm height. What is the depth of the ice-cream, correct to two decimal places?
m
3 cm
Ice-cream
6 cm
depth of
ice-cream
5cm

Answer 1

h = 5 cm

Explanation:

Given that,

The volume of ice-cream in the cone is half the volume of the cone.

Volume of cone is given by :

`V_c=(1)/(3)\pi r^2h`

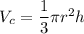
r is radius of cone, r = 3 cm

h is height of cone, h = 6 cm

So,

`V_c=(1)/(3)\pi (3)^2* 6\\\\V_c=18\pi\ cm^3`

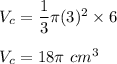
Let
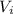`V_i` is the volume of icecream in the cone. So,

`V_i=(18\pi)/(2)=9\pi\ cm^3`

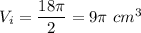
Let H be the depth of the icecream.

Two triangles formed by the cone and the icecream will be similiar. SO,

`(H)/(6)=(r)/(3)\\\\r=(H)/(2)`

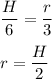
So, volume of icecream in the cone is :

`V_c=(1)/(3)\pi ((h)/(2))^2((h)/(3))\\\\9\pi=(h^3)/(12)\pi\\\\h^3=108\\\\h=4.76\ cm`

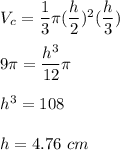
or

h = 5 cm

So, the depth of the ice-cream is 5 cm.