Question

Express the quotient of z1 and z2 in standard form given that
`z_(1) = -3[cos((-\pi )/(4) )+isin((-\pi )/(4) )]` and
`z_(2) = 2√(2) [cos((-\pi )/(2) )+isin((-\pi )/(2) )]`

Answer 1

Solution :
`-(3)/(4)-(3)/(4)i`

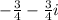
Explanation:

`-3\left[\cos \left((-\pi )/(4)\right)+i\sin \left((-\pi \:)/(4)\right)\right]\:/ \:2√(2)\left[\cos \left((-\pi \:\:)/(2)\right)+i\sin \left((-\pi \:\:\:)/(2)\right)\right]`

Let's apply trivial identities here. We know that cos(-π / 4) = √2 / 2, sin(-π / 4) = - √2 / 2, cos(-π / 2) = 0, sin(-π / 2) = - 1. Let's substitute those values,

`(-3\left((√(2))/(2)-(√(2))/(2)i\right))/(2√(2)\left(0-1\right)i)`

=
`-3\left((√(2))/(2)-(√(2))/(2)i\right)` ÷
`2√(2)\left(0-1\right)i`

=
`3\left(-(√(2)i)/(2)+(√(2))/(2)\right)` ÷
`-2√(2)i`

=
`(3\left(1-i\right))/(√(2))`÷
`2√(2)i` =
`-3-3i` ÷
`4` =
`-(3)/(4)-(3)/(4)i`

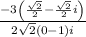
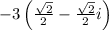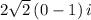
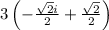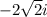
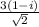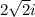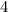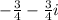
As you can see your solution is the last option.