Answer:
The height of the flag pole is approximately 19 feet and 2 inches.
Explanation:
Let suppose that length of the shadow of the object is directly proportional to its height. Hence:
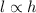
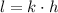
Where:
 - Height of the object, measured in inches.
- Height of the object, measured in inches.
 - Shadow length of the object, measured in inches.
- Shadow length of the object, measured in inches.
 - Proportionality constant, dimensionless.
- Proportionality constant, dimensionless.
Now, let is find the value of the proportionality constant: (
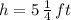 and
and
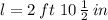 )
)
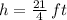
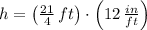
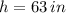

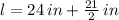
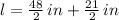
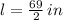
Then,
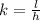
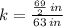
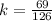
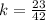
The equation is represented by
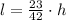 . If
. If
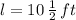 , then:
, then:
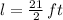


The height of the flag pole is: (
 ,
,
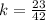 )
)
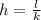
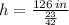
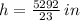
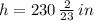

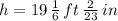
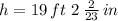
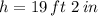
The height of the flag pole is approximately 19 feet and 2 inches.