Question

Suppose that 67.2% of all adults with type 2 diabetes also suffer from hypertension. After developing a new drug to treat type 2 diabetes, a team of researchers at a pharmaceutical company wanted to know if their drug had any impact on the incidence of hypertension for diabetics who took their drug. The researchers selected a random sample of 500 participants who had been taking their drug as part of a recent large-scale clinical trial and found that 317 suffered from hypertension.

The researchers want to use a one‑sample z ‑test for a population proportion to see if the proportion of type
2 diabetics who have hypertension while taking their new drug, p, is different from the proportion of all type
2 diabetics who have hypertension. They decide to use a significance level of ???? = 0.05.
A. Determine the p value for this test.
B. Determine the value of the z test statistic.

Answer 1

Answer: A. p-value = 0.04

B. z = - 1.77

Explanation: To calculate z test statistic or z-score for a population proportion, first find the proportion (p-hat):

`p_(hat)` =
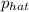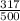`(317)/(500)` = 0.634

Then determine the standard deviation:

`\sigma = \sqrt{(p_(hat)(1-p_(hat)))/(n) }`

`\sigma = \sqrt{(0.634(0.366))/(500) }`

`\sigma = √(0.00046 )`

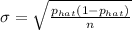
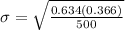
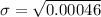
`\sigma` = 0.0215

Calculating z-score:

`z=(p_(hat)-p)/(\sigma)`

`z=(0.634-0.672)/(0.0215)`

`z=-1.77`

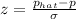
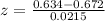
Z-test for the population proportion is z = - 1.77

P-value is the probability describing the data if null hypothesis is true, i.e.:

P(z< -1.77)

Using z-score table, the probability is:

P(z< -1.77) = 0.04

p-value = 0.04

P-value for this test is p-value = 0.04.