Question

Three faucets fill a 100-gallon tub in 6 minutes. How long, in seconds, does it take six faucets to fill a 25-gallon tub? Assume that all faucets dispense water at the same rate.

Answer 1

see below

Explanation:

It would take 3 faucets 6/4 = 1.5 minutes to fill a 25-gallon tub since when the number of faucets stays the same, the volume of the tub and the time needed to fill the tub are directly proportional. However, when the volume of the tub stays the same, the number of faucets used and the time needed to fill the tub are inversely proportional, therefore, if I double the number of faucets used, it will half the time needed, so the answer is 1.5 / 2 = 0.75 minutes or 45 seconds.

Answer 2

`\large\boxed{45 seconds}`

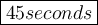
Explanation:

------------------------------------------------------------------------------------------------------------

Variable Key

Faucets = f

Minutes = m

Gallons = g

------------------------------------------------------------------------------------------------------------

Write an equation to display how long it takes for the 3 faucets to fill up a 100 gallon tub.

100g = 6m

Divide both sides of the equation by 6

m = 16.67g

This means that approximately 16.67 gallons are filled up per minute with 3 faucets. We found the measurement (gallons), which is based on the time (minutes). This is called the unit rate.

Now that we found the unit rate for 3 faucets, let's find the unit rate for 6 faucets by multiplying our unit rate by 2.

3f = 16.67g per minute

6f = (16.67g per minute)(2)

6f = 33.34 g per minute

We now know the unit rate for 6 faucets, so now all we have to do is divide that by 25 gallons, the second tub.

25g / 33.34 g = 0.75 minutes

Convert to seconds

0.75 minutes = 3/4 of a minute

1 minute = 60 seconds

Substitute

3/4(60)

`\large\boxed{45 seconds}`

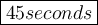
Hope this helps :)