Answer:
f(x) is quadratic. g(x) and h(x) are linear.
Explanation:
So we have the three functions:
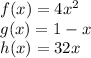
Linear functions are polynomials in which the highest degree is 1.
Quadratic functions are polynomials in which the highest degree is 2.
And exponential functions usually have a variable in the exponent (e.g. 2^x).
For f(x), the highest degree is 2. Thus, f(x) is a quadratic function.
For g(x), the highest degree is 1 and there are no variables in the exponent. Thus, g(x) is a linear function.
Similarly, for h(x), the highest degree is 1 and there are no variables in the exponents, so h(x) is also a linear function.