With dimensions x-by-y-by-z, the volume of such a box is
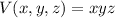
and its surface area is
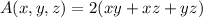
Given that A = 16 cm², we can solve for z in the constraint:
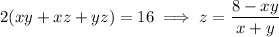
Substitute this into the volume function to reduce it to a function of 2 variables:
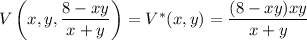
Find the critical points of V*, where both its partial derivatives vanish:
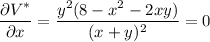
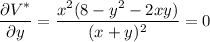
There's no box if either x = 0 or y = 0, so the critical points occur when
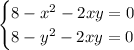
By combining the equations, we find
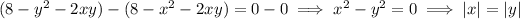
since √(x²) = |x| for any real x. But there's also no box if either x < 0 or y < 0, so by definition of absolute value, this condition reduces to
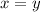
Substitute this into V* to once again reduce the number of variables:
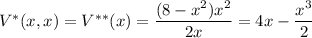
Find the critical points of V** :
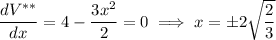
but again, x must be positive.
Putting everything together, there is only one critical point at
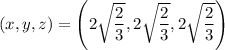
so the box with maximum area is a cube with side length 2√(2/3) ≈ 1.633 cm, with volume 16/3 √(2/3) ≈ 4.3547 cm³.
(Note that this problem is also amenable to using Lagrange multipliers, which might even save some work.)