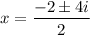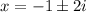Answer:
No real root.
Complex roots:
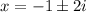
Explanation:
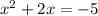
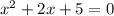
There are no two integers whose product is 5 and whose sum is 2, so this trinomial is not factorable. We can use the quadratic formula.
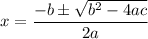
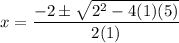
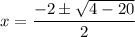
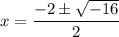
Since we have a square root of a negative number, there are no real roots. If you have learned complex numbers, then we can continue.