Question

If you have a 200g sample of a radioactive isotope that has a half life of 50 years, hc

much will you have left at the end of 200 years?
a. 12.5 g
b. 100 g
c. 50 g
d. 25 g

Answer 1

The correct option is;

a. 12.5 g

Step-by-step explanation:

The given parameters are;

The initial mass of the radioactive substance = 200 g

The half life of the radioactive substance = 50 years

The time duration for the disintegration = 200 years

The formula for half life is given as follows;

`N(t) = N_0 \left ((1)/(2) \right )^{(t)/(t_(1/2))`

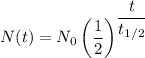
Where:

N(t) = Quantity of the remaining substance

N₀ = Initial radioactive substance quantity = 200 g

t = Time duration = 200 years

`t_(1/2)` = Half life of the radioactive substance 50 years

Therefore, we have;

`N(t) =200 * \left ((1)/(2) \right )^{(200)/(50) } =200 * \left ((1)/(2) \right )^4 = 12.5 \ g`

Therefore, at the end of 200 years, the quantity left = 12.5 g.