Question

An online polling site posed this question: "How much stock do you put in long-range weather forecasts?" Among its Web site users, 38, 528 chose to respond Complete parts (a) through (c) below.

a. Among the responses received, 3% answered with "a lot". What is the actual number of responses consisting of "a lot"?
b. Among the responses received, 18, 566 consisted of "very little or none". What percentage of responses consisted of "very little or none"?
c. Because the sample size of 38, 528 is so large, can we conclude that about 3% of the general population puts "a lot" of stock in long-range weather forecasts? Why or why not?
A. No, because the sample is a voluntary response sample, so the sample is not likely to be representative of the population.
B. Yes, because the sample is so large, the margin of error is negligible.
C. No, because even though the sample size is so large, there is still a margin of error.
D. Yes, because the sample size is large enough so that the sample is representative of the population.

Answer 1

(a) 1155.84

(b) 48.2%

(c) D

Explanation:

The number of total responses is, N = 38,528.

(a)

It is provided that 3% answered with "a lot".

Compute the actual number of responses consisting of "a lot" as follows:

n (a lot) = N × P (a lot)

= 38528 × 0.03

= 1155.84

Thus, the actual number of responses consisting of "a lot" is 1155.84.

(b)

The number of responses consisting of "very little or none" is,

n (very little or none) = 18,566

Compute the percentage of responses consisted of "very little or none" as follows:

`P(\text{very little or none})=\frac{n(\text{very little or none})}{N}`

`=(18566)/(38528)\\\\=0.481883\\\\\approx 0.482`

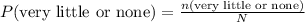
The percentage is: 0.482 × 100% = 48.2%.

Thus, the percentage of responses consisted of "very little or none" is 48.2%.

(c)

As the sample size increases the sample statistic value gets closer and closer to the actual population parameter value.

Thus, making the sample statistic an unbiased estimator of the population parameter.

And proving that the sample is a true representative of the population.

Thus, the correct option is (D).