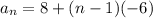Answer:
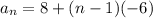
Explanation:
Given

Recursive:
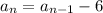
Required
Determine the formula
Substitute 2 for n to determine
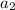
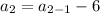
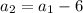
Substitute

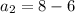
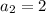
Next is to determine the common difference, d;
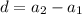
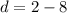
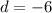
The nth term of an arithmetic sequence is calculated as

Substitute
 and
and
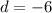

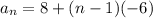
Hence, the nth term of the sequence can be calculated using