Question

How do I solve these equations:

sin(2θ) + sin θ = 0
sin(2θ) = sqrt 3 cos θ

for intervals 0=< θ < 2pi

Answer 1

Explanation:

Given that

sin(2θ)+sinθ=0

We know that

sin(2θ)=2 sinθ x cosθ

Therefore

2 sinθ x cosθ + sinθ=0

sinθ(2 cosθ+1)=0

sinθ= 0

θ=0

2 cosθ+1=0

cosθ= - 1/2

θ=120°

_______________________________________________________

`sin 2\theta=√(3cos\theta)`

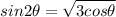
By squaring both sides

`sin^2 2\theta={3cos\theta}`

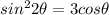
4 sin²θ x cos²θ=3 cosθ

4 sin²θ x cos²θ - 3 cosθ=0

cos θ = 0

θ= 90°

4 sin²θ=3

θ=60°