See attached sketch. Suppose the triangle is placed in the first quadrant of the coordinate plane, so the vertex y is at the origin, x is at the point (12, 0), and z is at the point (0, 6). Then the hypotenuse xz is contained in the line (12, 0) and (0, 6), with slope
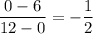
and hence equation
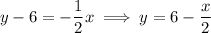
Since ∆xyd and ∆xyz have the leg xy in common, we'll let that be the base. Then the area of the ∆xyd is entirely determined by the vertical distance between the point d and the leg xy. ∆xyz has area 1/2 × 6 × 12 = 36, and so if we let d = (x', y'), we observe x' and y' are jointly distributed with density
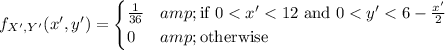
The area of ∆xyd is

and so we want to find
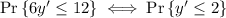
Now, the event that y' ≤ 2 can be split up into cases of
• 0 < x' ≤ 8 and 0 < y' ≤ 2
• 8 ≤ x' < 12 and 0 < y' < 6 - x'/2
So we have
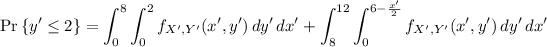
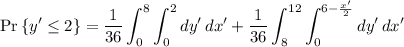
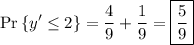
(i.e. the area of a trapezoid with base lengths 8 and 12 and height 2, divided by the total area of ∆xyz)