Answer:
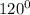
Explanation:
Given: pentagon (5 sided polygon), two interior angles =
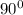 each, other three interior angles are congruent.
each, other three interior angles are congruent.
Sum of angles in a polygon = (n - 2) ×
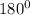
where n is the number of sides of the polygon.
For a pentagon, n = 5, so that;
Sum of angles in a pentagon = (5 - 2) ×
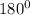
= 3 ×
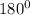
=
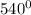
Sum of angles in a pentagon is
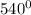 .
.
Since two interior angles are right angle, the measure of one of its three congruent interior angles can be determined by;
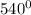 - (2 ×
- (2 ×
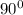 ) =
) =
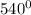 -
-
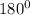
=
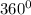
So that;
the measure of the interior angle =
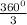
=
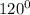
The measure of one of its three congruent interior angles is
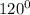 .
.