Question

Please answer quick Find the standard form of the equation of the parabola with a focus at (-2, 0) and a directrix at x = 2. (5 points) y^2 = 4x 8y = x^2 x = 1 divided by 8 y^2 y = 1 divided by 8 x^2

Answer 1

Explanation:

If you plot the focus and the directrix on a coordinate plane, because the parabola wraps itself around the focus away from the directrix, we know that this parabola opens to the left. That means its general form is

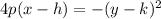`4p(x-h)=-(y-k)^2` where h and k are the coordinates of the vertex and p is the distance between the vertex and either the focus or the directrix because both distances are the same. Knowing that both distances are the same, it logically follows that the vertex is directly in between the focus and the directrix. So the vertex is at the origin, (0, 0). p is 2 because the vertex is at an x value of 0 and the directrix is at the x value of 2, and because the focus is at an x value of -2. Filling in the equation, then:

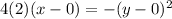`4(2)(x-0)=-(y-0)^2` which simplifies to

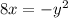`8x=-y^2` and, solving for x:

`x=-(1)/(8)y^2`