Answer:
40320 ways
Explanation:
Given
Paintings = 8
Required
Determine the number of arrangements
From the question, we understand that the order of arrangement matters;
This implies permutation and is calculated as thus;
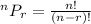
In this case,
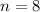
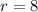 , because all paintings are hung;
, because all paintings are hung;
Substitute 8 for n and r, respectively
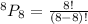
Evaluate the denominator
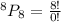
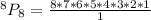
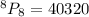
Hence, the number of arrangement is 40320 ways