Question

Maths!

1) Calculate the variance and standard division of the set of the data

2) If each value is added by 2, calculate the new standard deviation of the set

3) What is the effect on the measure of dispersion if each value is changed uniformly ​

Answer 1

(1) Variance = 4.5 and Standard deviation = 2.121.

(2) Variance = 4.5 and Standard deviation = 2.121.

(3) The effect on the measure of dispersion if each value is changed uniformly ​is that it remains unchanged.

Explanation:

We are given with the following set of data below;

X
`X-\bar X`
`(X-\bar X)^(2)`

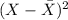
5 5 - 8 = -3 9

5 5 - 8 = -3 9

8 8 - 8 = 0 0

10 10 - 8 = 2 4

10 10 - 8 = 2 4

10 10 - 8 = 2 4

9 9 - 8 = 1 1

9 9 - 8 = 1 1

6 6 - 8 = -2 4

Total 72 36

Firstly, the mean of the above data is given by;

Mean,
`\bar X` =
`(\sum X)/(n)`

=
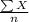
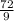`(72)/(9)` = 8

(1)Now, the variance of the given data is;

Variance =
`(\sum (X-\bar X)^(2) )/(n-1)`

=
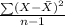
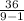`(36)/(9-1)` = 4.5

So, the standard deviation, (S.D.) =
`\sqrt{\text{Variance}}`

=
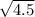`√(4.5)` = 2.12

(2) Now, each value is added by 2; so the new data set is given by;

X
`X-\bar X`
`(X-\bar X)^(2)`

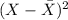
7 7 - 10 = -3 9

7 7 - 10 = -3 9

10 10 - 10 = 0 0

12 12 - 10 = 2 4

12 12 - 10 = 2 4

12 12 - 10 = 2 4

11 11 - 10 = 1 1

11 11 - 10 = 1 1

8 8 - 10 = -2 4

Total 90 36

Firstly, the mean of the above data is given by;

Mean,
`\bar X` =
`(\sum X)/(n)`

=
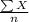
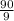`(90)/(9)` = 10

(1)Now, the variance of the given data is;

Variance =
`(\sum (X-\bar X)^(2) )/(n-1)`

=
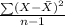
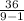`(36)/(9-1)` = 4.5

So, the new standard deviation, (S.D.) =
`\sqrt{\text{Variance}}`

=
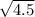`√(4.5)` = 2.12

(3) The effect on the measure of dispersion if each value is changed uniformly ​is that it remains unchanged as we see in the case of variance or standard deviation.