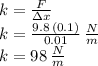Question

You need to make a spring scale to measure the mass of objects hung from it. You want each 1.0 cm length along the scale to correspond to a mass difference of 0.10 kg. What should be the value of the spring constant?

Answer 1

The spring constant should be:

`k= 98\, (N)/(m)`

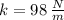
Step-by-step explanation:

Use Hooke's law for this problem, knowing that the magnitude of the force (F) on the spring equals the stretching it experiences
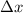`\Delta x` times the spring constant "k":

`F=k\,\Delta x`

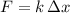
in our case, since the mass hanging is given in kg, we need to multiply it by "g" to get the force exerted:

Then if we add to the spring in its relaxed state, a mass of 0.10 kg, and we want for that a displacement of 1 cm (0.01 m), then the value of the spring constant should be:

`k=(F)/(\Delta x) \\k=(9.8\,(0.1))/(0.01) \, (N)/(m) \\k= 98\, (N)/(m)`