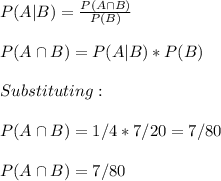Question

Find the missing probability. P(B)=720,P(A|B)=14 ,P(A∩B)=?

Answer 1

7/80

Explanation:

Given that: P(B) = 7 / 20, P(A|B)= 1 / 4

Bayes theorem is used to mathematically represent the conditional probability of an event A given B. According to Bayes theorem:

`P(A|B)=(P(A \cap B))/(P(B))`

Where P(B) is the probability of event B occurring, P(A ∩ B) is the probability of event A and event B occurring and P(A|B) is the probability of event A occurring given event B.

`P(A|B)=(P(A \cap B))/(P(B))\\\\P(A \cap B)=P(A|B)*P(B)\\\\Substituting:\\\\P(A \cap B)=1/4*7/20=7/80\\\\P(A \cap B)=7/80`