Answer:
the probability of no defects in 10 feet of steel = 0.1353
Explanation:
GIven that:
A roll of steel is manufactured on a processing line. The anticipated number of defects in a 10-foot segment of this roll is two.
Let consider β to be the average value for defecting
So;
β = 2
Assuming Y to be the random variable which signifies the anticipated number of defects in a 10-foot segment of this roll.
Thus, y follows a poisson distribution as number of defect is infinite with the average value of β = 2
i.e
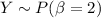
the probability mass function can be represented as follows:
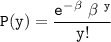
where;
y = 0,1,2,3 ...
Hence, the probability of no defects in 10 feet of steel
y = 0
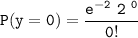

P(y =0) = 0.1353