Answer:
792.9 in²
Explanation:
Given:
Area of the base of the regular hexagonal prism box (B) = 85.3 in²
Each side length of hexagonal base (s) = 5.73 in
Height of prism box (h) = 18.10 in
Required:
Surface area of the wood used in making the hexagonal prism box
SOLUTION:
Surface area for any given regular prism can be calculated using the following formula: (Perimeter of Base × height of prism) + 2(Base Area)
Perimeter of the hexagonal base of the prism box = 6(5.73) (Note: hexagon has 6 sides.)
Perimeter of base = 34.38 in
Height = 18.10 in
Base area is already given as 85.3 in²
Surface area of the hexagonal prism box
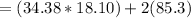
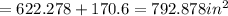
Surface area of the wood used in making the jewelry box ≈ 792.9 in²