Hello, n being an integer, we need to prove that one statement depending on n is true, let's note it S(n).
The mathematical induction involves two steps:
Step 1 - We need to prove S(1), meaning that the statement is true for n = 1
Step 2 - for k integer > 1, we assume S(k) and we need to prove that S(k+1) is true.
Imagine that you are a painter and you need to paint all the trees on one side of a road. You have several colours that you can use but you are asked to follow two rules:
Rule 1 - You need to paint the first tree in white.
Rule 2 - If one tree is white you have to paint the next one in white too.
What colour do you think all the trees will be painted?
Do you see why this is very important to prove the two steps as well ?
Let's do it in this example.
Step 1 - for n = 1, let's prove that S(1) is true, meaning
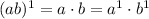
So the statement is true for n = 1
Step 2 - Let's assume that this is true for k, and we have to prove that this is true for k+1
So we assume S(k), meaning that
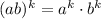
and what about S(k+1), meaning
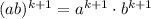 ?
?
We will use the fact that this is true for k,
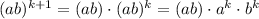
We can write it because the statement at k is true and then we can conclude.
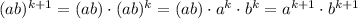
In conclusion, we have just proved that S(n) is true for any n integer greater or equal to 1, meaning
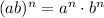
Hope this helps.
Do not hesitate if you need further explanation.
Thank you