Question

Find the sum of 1 + 3/2 + 9/4 + …, if it exists.

Answer 1

Option (4)

Explanation:

Given sequence is,

`1+(3)/(2)+(9)/(4)..........`

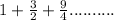
We can rewrite this sequence as,

`1+(3)/(2)+((3)/(2))^2.............`

There is a common ratio between the successive term and the previous term,

r =
`((3)/(2))/(1)`

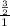
r =
`(3)/(2)`

Therefore, it's a geometric sequence with infinite terms. In other words it's a geometric series.

Since sum of infinite geometric sequence is represented by the formula,

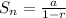`S_(n)=(a)/(1-r)` , when r < 1

where 'a' = first term of the sequence

r = common ratio

Since common ratio of the given infinite series is greater than 1 which makes the series divergent.

Therefore, sum of infinite terms of a series will be infinite Or the sum is not possible.

Option (4) will be the answer.