Question

Two trains leave New York at the same time heading in opposite directions. Train A travels at 4 5 the speed of train one. After seven hours they are 693 miles apart. What was the speed of train A?

Answer 1

Speed of train A is 44 miles/hr.

Explanation:

Let the speed of train A =
`u\ miles/hr`

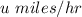
Let the speed of train one =
`v\ miles/hr`

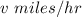
Train A travels at
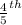`(4)/(5)^(th)` the speed of train one.

i.e.

`u = (4)/(5)v \\\Rightarrow v =(5)/(4)u.... (1)`

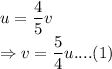
Distance traveled = 693 miles

Time taken = 7 hours

They are travelling in opposite directions so the resultant speed will appear to be faster.

Relative speed =
`u+v\ miles/hr`

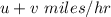
The trains are 693 miles apart in 7 hours that means they have traveled a total distance of 693 miles in 7 hours with a speed of (
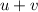`u+v`) miles/hr.

Using the formula:

`Speed = (Distance)/(Time)`

`u+v = (693)/(7)\\\Rightarrow u+v=99 ...... (2)`

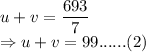
Putting the value of v using equation (1):

`\frac{5}4u+u=99\\\Rightarrow 5u+4u = 99 * 4\\\Rightarrow 9 u = 99 * 4\\\Rightarrow u = 11 * 4 = \bold{44\ miles/hr}`

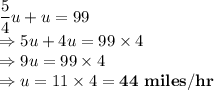
Speed of train A is 44 miles/hr.