Answer:
362880 ways
Explanation:
Given
10 digits
Required
Number of 10 digits that can be formed if no repetition and 2 must always start;
Since digit 2 must always start and no repetition is allowed, then there are 9 digits left
Digit 2 can only take 1 position
9 digits can be arranged without repetition in 9! ways;
Calculating 9!
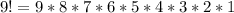
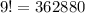
Number of arrangement = 1 * 362880
Number of arrangement = 362880 ways