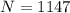Question

In a recent year, a sample of grade 8 Washington State public school students taking a mathematics assessment test had a mean score of 281 with a standard deviation of 34.4. Possible test scores could range from 0 to 500. Assume that the scores are normally distributed. Question 9 (2.5 points) If 2000 students are randomly selected, how many would you expect to have a score between 250 and 305?

Answer 1

The number is
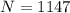`N =1147` students

Explanation:

From the question we are told that

The population mean is
`\mu = 281`

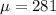
The standard deviation is
`\sigma = 34.4`

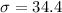
The sample size is n = 2000

percentage of the would you expect to have a score between 250 and 305 is mathematically represented as

`P(250 < X < 305 ) = P(( 250 - 281)/(34.4 ) < (X - \mu )/(\sigma ) < ( 305 - 281)/(34.4 ) )`

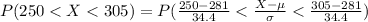
Generally

`(X - \mu )/(\sigma ) = Z (Standardized \ value \ of \ X )`

So

`P(250 < X < 305 ) = P(-0.9012< Z<0.698 )`

`P(250 < X < 305 ) = P(z_2 < 0.698 ) - P(z_1 < -0.9012)`

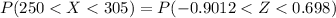
From the z table the value of
`P( z_2 < 0.698) = 0.75741`

and
`P(z_1 < -0.9012) = 0.18374`

`P(250 < X < 305 ) = 0.75741 - 0.18374`

`P(250 < X < 305 ) = 0.57`

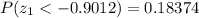
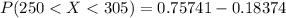
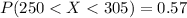
The percentage is
`P(250 < X < 305 ) = 57\%`

The number of students that will get this score is

`N = 2000 * 0.57`

`N =1147`