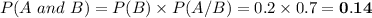Question

1) Given P(A) = 0.3 and P(B) = 0.5, do the following.

(a) If A and B are mutually exclusive events, compute P(A or B).
(b) If P(A and B) = 0.2, compute P(A or B).
2) Given P(A) = 0.4 and P(B) = 0.2, do the following.
(a) If A and B are independent events, compute P(A and B).
(b) If P(A | B) = 0.7, compute P(A and B).

Answer 1

1) a) 0.8

b) 0.6

2) a) 0.08

b) 0.14

Explanation:

1) Given

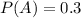`P(A) = 0.3` and
`P(B) = 0.5`

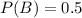
Let us learn about a formula:

`P(A\ or\ B) = P(A) +P(B) -P(A\ and\ B)\\OR\\P(A\cup B) = P(A) +P(B) -P(A\cap B)`

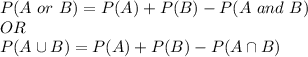
(a) If A and B are mutually exclusive i.e. no common thing in the two events.

In other words:

`P(A\ and\ B)` =
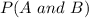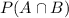`P(A \cap B)` = 0

Using above formula:

`P(A\ or\ B) = P(A) +P(B) -P(A\ and\ B)\\\Rightarrow P(A\ or\ B) = 0.3 + 0.5 -0 = \bold{0.8}`

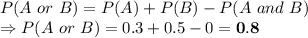
(b) P(A and B) = 0.2

Using above formula:

`P(A\ or\ B) = P(A) +P(B) -P(A\ and\ B)\\\Rightarrow P(A\ or\ B) = 0.3 + 0.5 -0.2 = \bold{0.6}`

*************************************

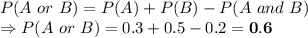
1) Given

`P(A) = 0.4` and
`P(B) = 0.2`

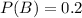
Let us learn about a formula:

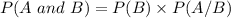`P(A\ and\ B) = P(B) * P(A/B)` for dependent events

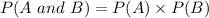`P(A\ and\ B) = P(A) * P(B)` for independent events.

(a) If A and B are independent events :

Using the above formula for independent events:

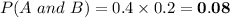
`P(A\ and\ B) = 0.4 * 0.2 = \bold{0.08}`

(b)
`P(A / B) = 0.7`

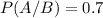
Using above formula:

`P(A\ and\ B) = P(B) * P(A/B) = 0.2 * 0.7 = \bold{0.14}`