Answer:
ΔABC ~ ΔQPR by the Angle-Angle (AA) similarity theorem of two triangles
Explanation:
The coordinates of the vertices are given as follows;
A = (1, 2), B =(9, 8), C = (1, 8)
P= (5, -3), Q = (-7, 6), R = (-7, -3)
The given dimensions of AB and PQ are 10, and 15 respectively
The, l lengths of the sides of triangles are found as follows;
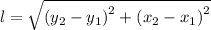
For segment BC, we have;
B =(9, 8), C = (1, 8)
(x₁, y₁) = (9, 8), (x₂, y₂) = (1, 8), substituting gives;
Length BC = 8
For length CA, C = (1, 8) A = (1, 2)
(x₁, y₁) = (1, 8)
(x₂, y₂) = (1, 2)
The length found by substituting the values for (x₁, y₁), (x₂, y₂) in the length equation gives; Length CA = 6
Given that length CA² + BC² = 8² + 6² = 64 + 36 = 100 = BA², we have by Pythagoras theorem, we have ΔABC is a right triangle
Similarly, for ΔQPR, we have;
Length QR, Q = (-7, 6), R = (-7, -3) = 9
Length PR, P= (5, -3), R = (-7, -3) = 12
QR² + PR² = 9² + 12² = 225 = 15² = PQ²
∴ ΔQPR is a right triangle
By comparing the ratio of the sides, we have;
cos(θ) = PR/PQ = 12/15 = 4/5, θ = cos⁻¹(4/5) = 36.9°
∠RPQ = 36.9°
sin(θ) = QR/PQ = 9/15 = 3/5
Similarly in triangle ΔABC, we have;
cos(θ) = BC/AB = 8/10 = 4/5
∠CBA = 36.9°
Therefore, ∠CBA ≅ ∠RPQ = 36.9°
Also ∠PRQ ≅ ∠BCA = 90° (Angle opposite hypotenuse side of right triangle
Therefore, ΔABC and ΔQPR are similar triangles by the Angle-Angle (AA) similarity theorem of two triangles.