Answer:
The shortest altitude is 6.72 cm
Explanation:
Given that the side lengths are
24 cm, 25 cm, 7 cm
The area of a triangle =
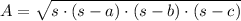
Where;
s = Half the perimeter = (24 + 25 + 7)/2 = 28
A = √((28×(28 - 24)×(28 - 25)×(28 - 7)) = 84 cm²
We note that 84/7 = 12
Therefore, the triangle is a right triangle with hypotenuse = 25, and legs, 24 and 7, the height of the triangle = 7
To find the shortest altitude, we utilize the formula for the area of the triangle A = 1/2 base × Altitude
Altitude = A/(1/2 ×base)
Therefore, the altitude is inversely proportional to the base, and to reduce the altitude, we increase the base as follows;
We set the base to 25 cm to get;
Area of the triangle A = 1/2 × base × Altitude
84 = 1/2 × 25 × Altitude
Altitude = 84/(1/2 × 25) = 6.72 cm
The shortest altitude = 6.72 cm.