Question

Your first baby was born yesterday and is healthy and strong. To guard against your premature death, you want to purchase a life insurance policy that will replace $58,000 of your annual income until your child is 20 years old. How much life insurance should you purchase, if you assume a 3% inflation rate

Answer 1

assuming the interest rate is = 15% the life insurance should you should purchase = $497854.0773

Step-by-step explanation:

Given that :

Annual income receipt = $58000

Assumption:

If we assume that the inflation rate π = 3% = 0.03

Also , let assume that the interest rate is = 15% = 0.15 since it is not given too

Then the effective interest rate =
`( (i-\pi))/((1+\pi))`

the effective interest rate =
`( (0.15-0.03))/((1+0.03))`

the effective interest rate =
`( (0.12))/((1.03))`

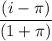
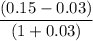
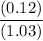
the effective interest rate = 0.1165

the effective interest rate = 11.65%

Since n =
`\infty`

The Principal amount of how much life insurance should you purchase is;

= Annual income receipt/the effective interest rate

= $58000/ 0.1165

= $497854.0773