Question

Does the function satisfy the hypotheses of the Mean Value Theorem on the given interval? f(x) = 4x2 − 3x + 2, [0, 2]

Answer 1

Yes , it satisfies the hypothesis and we can conclude that c = 1 is an element of [0,2]

c = 1 ∈ [0,2]

Explanation:

Given that:

`f(x) = 4x^2 -3x + 2, [0, 2]`

which is read as the function of x = 4x² - 3x + 2 along the interval [0,2]

Differentiating the function with respect to x is;

f(x) = 8x - 3

Using the Mean value theorem to see if the function satisfies it, we have:

`f'c = (f(b)-f(a))/(b-a)`

`8c -3 = (f(2)-f(0))/(2-0)`

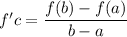
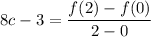
since the polynomial function is differentiated in [0,2]

`8c -3 = ((4(2)^2-3(2)+2)-(4(0)^2-3(0)+2))/(2-0)`

`8c -3 = ((4(4)-3(2)+2)-(4(0)-3(0)+2))/(2-0)`

`8c -3 = ((16-6+2)-(0-0+2))/(2-0)`

`8c -3 = ((12)-(2))/(2)`

`8c -3 = (10)/(2)`

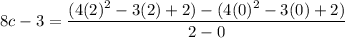
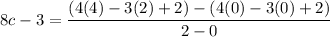
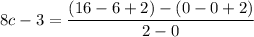
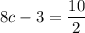
8c -3 = 5

8c = 5+3

8c = 8

c = 8/8

c = 1

Therefore, we can conclude that c = 1 is an element of [0,2]

c = 1 ∈ [0,2]