Question

What is the answer, what are the steps to solve this, and what do the parts of the equation represent?

Answer 1

`\sum_(a=1)^(7)(500-a)=3472`

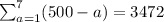
Explanation:

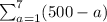`\sum_(a=1)^(7)(500-a)` will form a sequence as,

499, 498, 497.......7 terms

Since there is a common difference between successive and previous term,

d = 498 - 499 = -1

This sequence is an arithmetic sequence.

Sum of n terms of an arithmetic sequence is,

`S_(n)=(n)/(2)[2a+(n-1)d]`

where a = first term of the sequence

n = number of term

d = common difference

For the given given sequence,

`S_(7)=(7)/(2)[2(499)+(7-1)(-1)]`

=
`(7)/(2)[998-6]`

=
`(7)/(2)(992)`

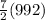
= 3472

Therefore, sum of seven terms of the given sequence will be 3472.