Question

Help asap (like right now )​

Answer 1

B) Yes, because the slope is
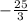`-(25)/(3)` and the zero is (12, 0)

Explanation:

From inspection of the graph:

• y-intercept = (0, 100)
• Two points: (3, 75) and (6, 50)

`\sf slope\:(m)=(change\:in\:y)/(change\:in\:x)=(50-75)/(6-3)=-(25)/(3)`

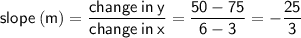
Therefore, the equation of the line in slope-intercept form y = mx + b

(where m is the slope and b is the y-intercept) is:

`y=-(25)/(3)x+100`

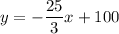
To find the zero (when y = 0), set the equation to zero and solve for x:

`\implies -(25)/(3)x+100=0`

`\implies (25)/(3)x=100`

`\implies 25x=300`

`\implies x=12`

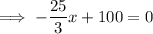
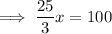
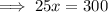
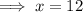
Therefore, the zero is at (12, 0)

Therefore, the graph does represent the function because the slope is
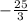`-(25)/(3)` and the zero is at (12, 0)