Answer: The number of sets contain any 4 numbers = 210
Explanation:
Given: Universal set = {0,1,2,3,4,5,6,7,8,9}.
i.e. Total choices = Numbers in set = 10
By combinations, the number of sets contain any 4 numbers =
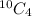
![=(10!)/(4!6!)\ \ \ \ \ [^nC_r=(n!)/(r!(n-r)!)]\\\\=(10*9*8*7*6!)/(4*3*2*1 *6!)\\\\=210](https://img.qammunity.org/2021/formulas/mathematics/high-school/vxslafpozrpydph8vrkv2oqhkv29zw1x4w.png)
Hence, the number of sets contain any 4 numbers = 210