Answer:
y = 20.99 V / A
there is no friction y = 20.99 h
Step-by-step explanation:
Let's solve this exercise in parts: first find the thrust on the block when it is submerged and then use the conservation of energy
when the block of ice is submerged it is subjected to two forces its weight hydrostatic thrust
F_net= ∑F = B-W
the expression stop pushing is
B = ρ_water g V_ice
where rho_water is the density of pure water that we take as 1 10³ kg / m³ and V is the volume d of the submerged ice
We can write the weight of the body as a function of its density rho_hielo = 0.913 10³ kg / m³
W = ρ-ice g V
F_net = (ρ_water - ρ_ ice) g V
this is the net force directed upwards, we can find the potential energy with the expression
F = -dU / dy
ΔU = - ∫ F dy
ΔU = - (ρ_water - ρ_ ice) g ∫ (A dy) dy
ΔU = - (ρ_water - ρ_ ice) g A y² / 2
we evaluate between the limits y = 0, U = 0, that is, the potential energy is zero at the surface
U_ice = (ρ_water - ρ_ ice) g A y² / 2
now we can use the conservation of mechanical energy
starting point. Ice depth point
Em₀ = U_ice = (ρ_water - ρ_ ice) g A y² / 2
final point. Highest point of the block
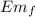 = U = m g y
= U = m g y
as there is no friction, energy is conserved
Em₀ = Em_{f}
(ρ_water - ρ_ ice) g A y² / 2 = mg y
let's write the weight of the block as a function of its density
ρ_ice = m / V
m = ρ_ice V
we substitute
(ρ_water - ρ_ ice) g A y² / 2 = ρ_ice V g y
y = ρ_ice / (ρ_water - ρ_ ice) 2 V / A
let's substitute the values
y = 0.913 / (1 - 0.913) 2 V / A
y = 20.99 V / A
This is the height that the lower part of the block rises in the air, we see that it depends on the relationship between volume and area, which gives great influence if there is friction, as in this case it is indicated that there is no friction
V / A = h
where h is the height of the block
y = 20.99 h