Question

A triangle has sides of lengths 16, 63, and 65. Is it a right triangle? Explain.

Answer 1

Yes

Explanation:

If a triangle is a right triangle, the 3 side lengths will check out in the Pythagorean Theorem.

`a^2+b^2=c^2`

where a and b are the legs and c is the hypotenuse.

The legs are the 2 shorter lengths and the hypotenuse is the longest length. The 3 side lengths are: 16,63 and 65. Therefore, 16 and 63 are the legs and 65 is the hypotenuse.

a=16

b=63

c=65

`16^2+63^2=65^2`

Evaluate each exponent.

16^2=16*16=256

`256+63^3=65^2`

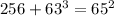
63^2=63*63=3969

`256+3969=65^2`

65^2=65*65=4225

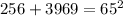
`256+3969= 4225`

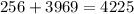
Add 256 and 3969

`4225=4225`

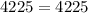
The statement above is true; 4225 is equal to 4225. Therefore, this is a right triangle because the side lengths check out when plugged into the Pythagorean Theorem.