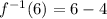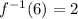Question

Suppose a function f has an inverse. If f(2)=6 and f(3)=7, find: f−1(6)

Answer 1

`f^(-1)(6) = 2`

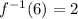
Explanation:

Given

`f(2) = 6`

`f(3) = 7`

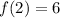
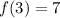
Required

`f^(-1)(6)`

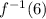
First, we need to determine the slope of the function using;

`m = (y_1 - y_2)/(x_1 - x_2)`

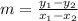
From the given parameters;

In
`f(2) = 6`

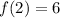
x = 2; y =6 --- Take this as x1 and y1

In
`f(3) = 7`

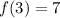
x = 3; y = 7 --- Take this as x2 and y2

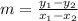`m = (y_1 - y_2)/(x_1 - x_2)` becomes

`m = (6 - 7)/(2 - 3)`

`m = (- 1)/( - 1)`

`m = 1`

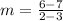
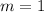
Next, we determine the equation of the function using

`y - y_1 = m(x - x_1)`

Substitute the values of x1,y1 and m

`y - 6 = 1(x - 2)`

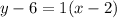
Open bracket

`y - 6 = x - 2`

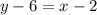
Add 6 to both sides

`y - 6 + 6 = x -2 +6`

`y = x + 4`

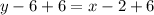
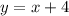
Next is to determine the inverse function by swapping the positions of x and y

`x = y + 4`

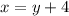
Make y the subject of formula;

`y = x - 4`

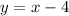
Replace y with
`f^(-1)(x)`

`f^(-1)(x) = x - 4`

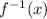
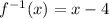
Now, we can solve for
`f^(-1)(6)`

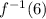
Substitute 6 for x

`f^(-1)(6) = 6 - 4`

`f^(-1)(6) = 2`