Question

A string passing over a smooth pulley carries a stone at one end. While its other end is attached to a vibrating tuning fork and the string vibrates forming 8 loops. When the stone is immersed in water 10 loops are formed. The specific gravity of the stone is close to

A)  1.8
B)  4.2
C)  2.8
D)  3.2​

Answer 1

correct option is C) 2.8

Explanation:

given data

string vibrates form = 8 loops

in water loop formed = 10 loops

solution

we consider mass of stone = m

string length = l

frequency of tuning = f

volume = v

density of stone =
`\rho`

case (1)

when 8 loop form with 2 adjacent node is
`(\lambda )/(2)`

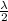
so here

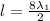`l = (8 \lambda _1)/(2)` ..............1

`l = 4 \lambda_1\\\\\lambda_1 = (l)/(4)`

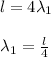
and we know velocity is express as

velocity = frequency × wavelength .....................2

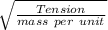`\sqrt{(Tension)/(mass\ per\ unit \length )}` = f ×
`\lambda_1`

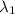
here tension = mg

so

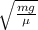`\sqrt{(mg)/(\mu)}` = f ×
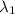`\lambda_1` ..........................3

and

case (2)

when 8 loop form with 2 adjacent node is
`(\lambda )/(2)`

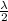
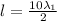`l = (10 \lambda _1)/(2)` ..............4

`l = 5 \lambda_1\\\\\lambda_1 = (l)/(5)`

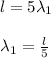
when block is immersed

equilibrium eq will be

Tenion + force of buoyancy = mg

T + v ×
`\rho` × g = mg

and

T = v ×
`\rho` - v ×
`\rho` × g

from equation 2

f ×
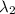`\lambda_2` = f ×
`(1)/(5)`

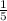
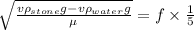`\sqrt{(v\rho _(stone) g - v\rho _(water) g)/(\mu)} = f * (1)/(5)` .......................5

now we divide eq 5 by the eq 3

`\sqrt{(vg (\rho _(stone) - \rho _(water)))/(\mu vg * \rho _(stone))} = (fl)/(5) * (4)/(fl)`

solve irt we get

`1 - (\rho _(stone))/(\rho _(water)) = (16)/(25)`

so

relative density
`(\rho _(stone))/(\rho _(water)) = (25)/(9)`

relative density = 2.78 ≈ 2.8

so correct option is C) 2.8