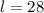Answer:
Explanation:
Given
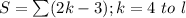
Required
What is l when S = 725
This can be solved using Sum of n terms of an AP;
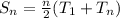
Where

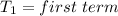
To get T1; we substitute 4 for k in 2k - 3
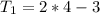
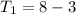
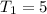
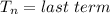
To get Tn; we substitute l for k in 2k - 3
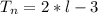
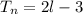
n = the number of terms;
Since k = 4 to l, then
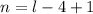
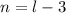
Substitute these values in
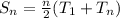
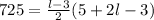
Collect Like Terms
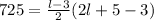
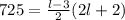
Open the bracket
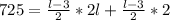
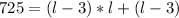
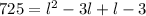
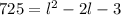
Subtract 725 from both sides
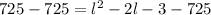
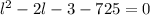
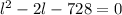
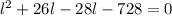
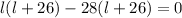
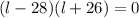
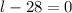 or
or
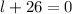
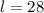 or
or
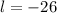
But l must be positive;
Hence,