Question

5. A combination of waves is producing oscillations on a rope that is fixed at both ends and has a tension of 100 ????. The wavelength of the resulting net wave is equal to the length of the rope. If the equation for the displacement of a point on the rope is given by y(x, t) = (0.1 m) sin π x sin 12πt, where the rope begins at x = 0, x is in meters, and t is in seconds, what are the a) length of the rope, b) the speed of the waves on the rope, and c) the mass of the rope?

Answer 1

a) 4 m

b) 24 m/s

c) 0.174 kg

Step-by-step explanation:

a) Tension in string equation

The information given are;

The wavelength is equal to the rope length , λ = L

The tension = 100 N

The displacement of a point on the rope is y(x, t) = (0.1 m) sinπ x sin 12πt

Given that the wavelength = the length of the rope, the rope is on second harmonic

L = 2·n and the length of the wire = 2 × 2 = 4 m given the dimensions are in meters

b) Where k = 2·π/λ

v = ω/k = 12π/(2·π/λ)= (12π/2π)×λ = 24 m/s

c) f = v/λ = 24/4 = 6 Hz

`f = \frac{\sqrt{(T)/(m/L) } }{2L} = \frac{\sqrt{(100)/(m/4) } }{2 * 4}`

`6 * 8= {\sqrt{(100)/(m/4) } }`

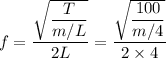
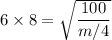
m/4 = 100/2304

m = 0.174 kg.