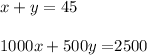Question

A business has $25,000 to spend on training sessions for its employees. It wants 45 of its employees to attend. The business wants to send as many employees as it can to a technology training. The technology training costs $1,000 per person. The customer service training costs $500 per person. Create a system of equations that models how many of each type of training the business should purchase. 1,000x + 500y = 45 x + y = 25,000 1,000x + 500y = 25,000 x + y = 45 1,000x + y = 45 x + 500y = 25,000 x + 500y = 45 1,000x + y = 25,000

Answer 1

1,000x + 500y = 45

x + y =45

Explanation:

So that means answer b is the correct answer, also I took the test.

Answer 2

Answer:
`x+y=45\\\\1000 x + 500y = $2500`

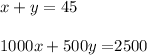
Explanation:

Let x = Number of employees taking technology training

y= Number of employees taking customer service training

Given, The technology training costs $1,000 per person. The customer service training costs $500 per person.

Total cost = 1000 x + 500y

Since, Total cost = $25,000 and total employee to attend training= 45 .

That means , the required equations are:

`x+y=45\\\\1000 x + 500y = $2500`