Question

An urn contains two blue balls (denoted B1 and B2) and three white balls (denoted W1, W2, and W3). One ball is drawn, its color is recorded, and it is replaced in the urn. Then another ball is drawn and its color is recorded.

a. Let B1 W2 denote the outcome that the first ball drawn is B1 and the second ball drawn is W2. Because the first ball is replaced before the second ball is drawn, the outcomes of the experiment are equally likely. List all 25 possible outcomes of the experiment.

b. Consider the event that the first ball that is drawn is blue. List all outcomes in the event. What is the probability of the event?

c. Consider the event that only white balls are drawn. List all outcomes in the event. What is the probability of the event?

Answer 1

(a) Shown below.

(b) The probability that the first ball drawn is blue is 0.40.

(c) The probability that only white balls are drawn is 0.36.

Explanation:

The balls in the urn are as follows:

Blue balls: B₁ and B₂

White balls: W₁, W₂ and W₃

It is provided that two balls are drawn from the urn, with replacement, and their color is recorded.

(a)

The possible outcomes of selecting two balls are as follows:

B₁B₁ B₂B₁ W₁B₁ W₂B₁ W₃B₁

B₁B₂ B₂B₂ W₁B₂ W₂B₂ W₃B₂

B₁W₁ B₂W₁ W₁W₁ W₂W₁ W₃W₁

B₁W₂ B₂W₂ W₁W₂ W₂W₂ W₃W₂

B₁W₃ B₂W₃ W₁W₃ W₂W₃ W₃W₃

There are a total of N = 25 possible outcomes.

(b)

The sample space for selecting a blue ball first is:

S = {B₁B₁, B₁B₂, B₁W₁, B₁W₂, B₁W₃, B₂B₁, B₂B₂, B₂W₁, B₂W₂, B₂W₃}

n (S) = 10

Compute the probability that the first ball drawn is blue as follows:

`P(\text{First ball is Blue})=(n(S))/(N)=(10)/(25)=0.40`

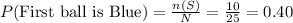
Thus, the probability that the first ball drawn is blue is 0.40.

(c)

The sample space for selecting only white balls is:

X = {W₁W₁, W₂W₁, W₃W₁, W₁W₂, W₂W₂, W₃W₂, W₁W₃, W₂W₃, W₃W₃}

n (X) = 9

Compute the probability that only white balls are drawn as follows:

`P(\text{Only White balls})=(n(X))/(N)=(9)/(25)=0.36`

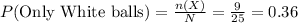
Thus, the probability that only white balls are drawn is 0.36.