Answer:
A. unbiased estimator.
Explanation:
In Statistics, an estimator is a statistical value which is used to estimate a parameter. Parameters are the determinants of the probability distribution. Therefore, to determine a normal distribution we would use the parameters, mean and variance of the population.
A function of random variables used to estimate a parameter of a distribution is an unbiased estimator.
An unbiased estimator is one in which the difference between the estimator and the population parameter grows smaller as the sample size grows larger. This simply means that, an unbiased estimator captures the true population value of the parameter on average, this is because the mean of its sampling distribution is the truth.
Also, we know that the bias of an estimator (b) that estimates a parameter (p) is given by;
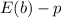
Hence, an unbiased estimator is an estimator that has an expected value that is equal to the parameter i.e the value of its bias is equal to zero (0).
Generally, in statistical analysis, sample mean is an unbiased estimator of the population mean while the sample variance is an unbiased estimator of the population variance.