Question

I need help please will give you 5 stars and good rating

Answer 1

x=12

Explanation:

To solve for the variable, we must isolate the variable, which is x.

`√(x+4) -3=1`

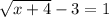
3 is being subtracted from the square root of x+4. The inverse of subtraction is addition. Add 3 to both sides of the equation.

`√(x+4) -3+3=1+3`

`√(x+4) =1+3`

`√(x+4) =4`

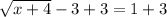
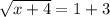
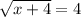
The square root of x+4 is being taken. The inverse of a square root is a square. Square both sides of the equation.

`(√(x+4))^2 =4^2`

`x+4=4^2`

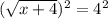
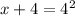
Evaluate the exponent.

4^2= 4*4=16

`x+4=16`

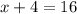
4 is being added to x. The inverse of addition is subtraction. Subtract 4 from both sides of the equation.

`x+4-4=16-4`

`x=16-4`

`x=12`

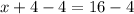
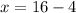
The solution to this equation is x=12.

Answer 2

Explanation: